均衡化2D
功能介绍
模块位置:图像处理-均衡化2D
支持对图像进行直方图均衡化、光源均衡化(降低图像中心相对四周的亮度);
直方图均衡化
通过重新分配像素的灰度值,使输出图像的灰度直方图近似均匀分布。其核心操作是使用原图像灰度级的累积分布函数(CDF) 作为映射函数。首先计算灰度级概率分布 (Probability Density Function, PDF):
- : 第 级灰度值
- : 图像中灰度值为 的像素个数
- : 图像的总像素数(图像高度M × 宽度N)
- : 灰度级 出现的概率(即其“权重”)
- :灰度级数,如8bit图像为256
然后计算累积分布函数 (Cumulative Distribution Function, CDF):
- : 变换后的新灰度值(归一化到 [0, 1] 区间)
最终将CDF值 线性映射到新的灰度级:
- :四舍五入到最近的整数,确保结果为离散灰度级。
- :最大灰度值(如8位图像为255)
示例:
 | 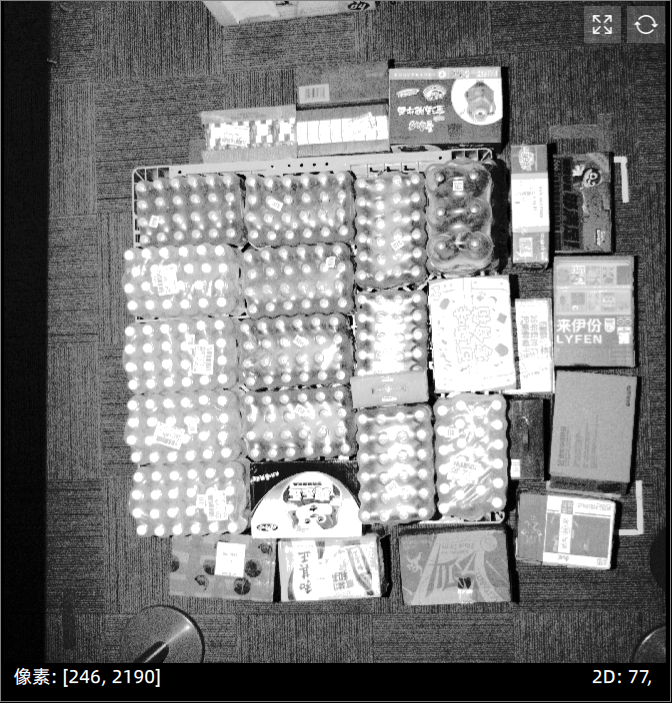 |
|---|---|
| 原图 | 直方图均衡化结果 |
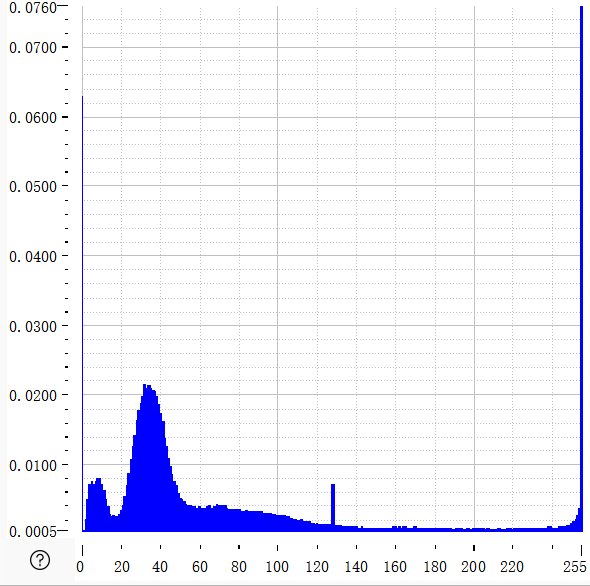 | 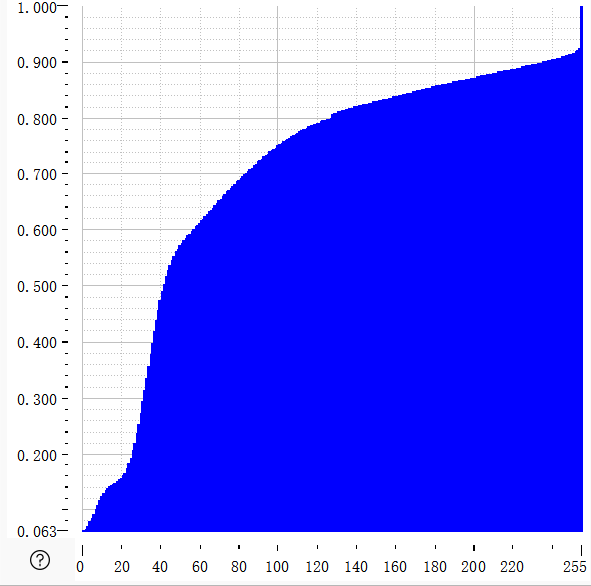 | 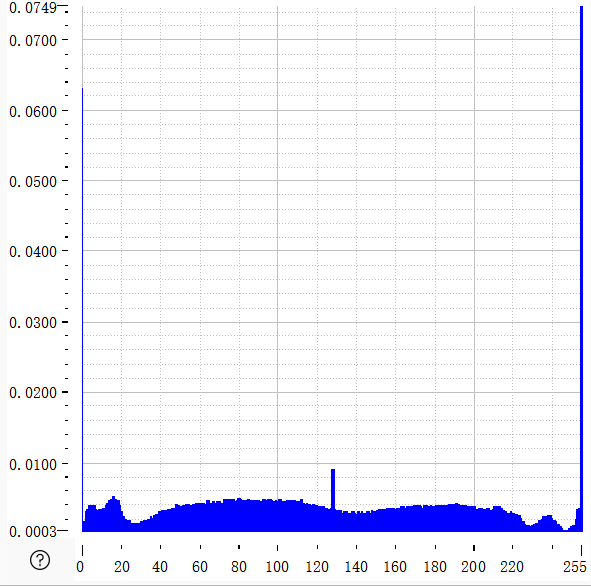 |
|---|---|---|
| 原灰度概率分布 | 灰度累计概率分布 | 均衡化后灰度概率分布 |
光源均衡化
朗伯余弦定律描述了理想漫反射表面(朗伯体)的表观亮度如何随观察角度(或照明角度)变化的规律。该定律指出:一个朗伯体在任意方向上的辐射强度与观察方向和表面法线之间夹角的余弦成正比。对于一个被均匀照明的理想漫反射表面,其表现亮度遵循以下公式:
- : 观察者感知到的表面亮度(辐射强度或光强);
- : 光源垂直入射 () 时表面的最大亮度;
- : 光源入射方向与物体表面法线方向之间的夹角;
假设被摄物表面垂直于相机光心,当存在中心光源时,大视野范围物体在相机里成像结果呈现中心亮四周暗现象;使用作为增益因子对理论光学衰减进行补偿,期望改善这种亮度不均匀;
其中,r 是像素点到图像中心的归一化距离(),θ 是该点对应的离轴角,计算依赖相机的标定参数。
示例:
 |  |  |
|---|---|---|
| 原图 | 增益图像 | 光源均衡化结果 |
使用场景
用于改善应用场景中2D图像的亮度不均匀或点光源中心过曝问题;
输入
| 输入 | 类型 | 说明 |
|---|---|---|
| 图像源 | 图像 | 输入图像 |
输出
| 输出 | 类型 | 默认启用 | 额外启用条件 | 说明 |
|---|---|---|---|---|
| 输出图像 | 图像 | 是 | / | 处理后的图像 |